Elastic Collision in One Dimension:
When both momentum and kinetic energy are conserved in a collision, then collision is called elastic collision.
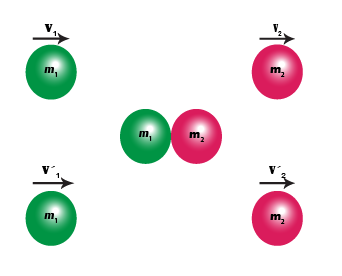 Consider two smooth non-rotating balls of masses m1 mass m2 moving initially with velocities v1 and v2 in the same direction.
We assume that v1 > v2 .
Therefore m1 will come close to m2 and will collide with it.
After collision they move along the same straight line without rotation. Let their velocities after the collision be v’1 and v’2 respectively.
Consider two smooth non-rotating balls of masses m1 mass m2 moving initially with velocities v1 and v2 in the same direction.
We assume that v1 > v2 .
Therefore m1 will come close to m2 and will collide with it.
After collision they move along the same straight line without rotation. Let their velocities after the collision be v’1 and v’2 respectively.
We take the positive direction of the velocity and momentum to the right. By applying the law of conservation of momentum we have
$$ m_{1}v_{1} + m_{2}v_{2} = m_{1}{v}'_{1} + m_{2}{v}'_{2} $$
$$m_{1}(v_{1} – {v}'_{1}) = m_{2}(v_{2} – {v}'_{2}) \;\;\;\; \cdot \cdot\cdot\cdot (1)$$
As the collision is elastic, so the K.E is also conserved.
From the conservation of K.E we have
$$\frac{1}{2}m_{1} {v_{1}}^2 + \frac{1}{2}m_{2} {v_{2}}^2 = \frac{1}{2}m_{1} {{v}'_{1}}^2 + \frac{1}{2}m_{2} {{v}'_{2}}^2
$$ $$
m_{1}( {v_{1}}^2 - {{v}'_{1}}^2) = m_{2} ( {{v}'_{2}}^2 - {v_{2}}^2)
$$ $$
m_{1}( v_{1} + {v}'_{1}) ( v_{1} - {v}'_{1})= m_{2} ( {v}'_{2} + v_{2}) ( {v}'_{2} - v_{2})\;\;\;\; \cdot \cdot\cdot\cdot (2) $$
Dividing eq 2 by eq 1
$$
m_{1}( v_{1} + {v}'_{1}) ( v_{1} - {v}'_{1})= m_{2} ( {v}'_{2} + v_{2}) ( {v}'_{2} - v_{2}) $$
$$ ( v_{1} + {v}'_{1}) = ( {v}'_{2} + v_{2}) $$
$$ ({v}_{1}- v_{2})= ({v}'_{2} – {v}'_{1}) = -( {v}'_{1} – {v}'_{2})$$
we note that , before collision, (v1 – v2) is the velocity of the first ball relative to second ball. Similarly ( v'1 – v'2) is the velocity of first ball relative to the second ball after collision. It means that relative velocities before and after the collision have the same magnitude but are reversed after the collision.
In other words, the magnitude of relative velocity of approach is equal to the magnitude of relative velocity of separation.
In eq 1 and 2 m1, m2, v1 and v2 are known quantities. We solve these equations to find the values of v’1 and v’2 which are unknown.
From equation 2
$$
v'_{2} = v_{1}+v'_{1}-v_{2}
$$
putting this in eq 2
$$
m_{1}v_{1} + m_{2}v_{2}= m_{1}v'_{1}+ m_{2}v_{1}+m_{2}v'_{1}-m_{2}v_{2}
$$ $$
m_{1}v'_{1}+m_{2}v'_{1} = m_{1}v_{1}+m_{2}v_{2}-m_{2}v_{1}+m_{2}v_{2} $$ $$
(m_{1}+m_{2}) v'_{1} = (m_{1}-m_{2})v_{1}+2m_{2}v_{2}
$$ $$
v'_{1}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} + \frac{2m_{2}v_{2}}{m_{1}+m_{2}} \;\;\;\; \cdot \cdot \cdot \cdot (3)$$
Similarly
$$v'_{1} = v'_{2}-v_{1}+v_{2}
$$ $$
m_{1}v_{1}+m_{2}v_{2}= m_{1}v'_{1} + m_{2}v'_{2}
$$ $$
m_{1}v_{1}+m_{2}v_{2}= m_{1}(v'_{2}-v_{1}+v_{2}) + m_{2}v'_{2} $$ $$
m_{1}v_{1}+m_{2}v_{2}= m_{1}v'_{2}-m_{1}v_{1}+m_{1}v_{2} + m_{2}v'_{2} $$ $$
m_{1}v_{1}+m_{1}v_{1}+m_{2}v_{2}-m_{1}v_{2} = m_{1}v'_{2} + m_{2}v'_{2} $$ $$
2m_{1}v_{1}+m_{2}v_{2}-m_{1}v_{2} = (m_{1} + m_{2})v'_{2}
$$ $$ 2m_{1}v_{1}+(m_{2}-m_{1})v_{2} = (m_{1} + m_{2})v'_{2}
$$ $$
v'_{2}= \frac{2m_{1}}{m_{1} + m_{2}}v_{1} + \frac{m_{2}-m_{1}}{m_{1} + m_{2}}
$$ $$
v'_{2}= \frac{2m_{1}}{m_{1} + m_{2}}v_{1} - \frac{m_{1}-m_{2}}{m_{1} + m_{2}}
$$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{2}}v_{1} +\frac{m_{2}-m_{1}}{m_{1}+m_{2}}v_{2} \;\;\;\; \cdot \cdot \cdot \cdot (4)$$
There are some cases of special interest, which are discusses below:
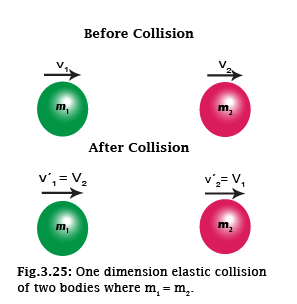
- when m1 = m2
 $$
v'_{1}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} + \frac{2m_{2}v_{2}}{m_{1}+m_{2}}
$$ $$
v'_{1}=\frac{m_{1}-m_{1}}{m_{1}+m_{1}}v_{1} + \frac{2m_{1}v_{2}}{m_{1}+m_{1}}
$$ $$
v'_{1}=\frac{0}{m_{1}+m_{1}}v_{1} + \frac{2m_{1}v_{2}}{2m_{1}}$$
from above equations we find that
$$ {v}’_{1} = v_{2}$$
and $$ {v}’_{2} = v_{1}$$
$$
v'_{1}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} + \frac{2m_{2}v_{2}}{m_{1}+m_{2}}
$$ $$
v'_{1}=\frac{m_{1}-m_{1}}{m_{1}+m_{1}}v_{1} + \frac{2m_{1}v_{2}}{m_{1}+m_{1}}
$$ $$
v'_{1}=\frac{0}{m_{1}+m_{1}}v_{1} + \frac{2m_{1}v_{2}}{2m_{1}}$$
from above equations we find that
$$ {v}’_{1} = v_{2}$$
and $$ {v}’_{2} = v_{1}$$
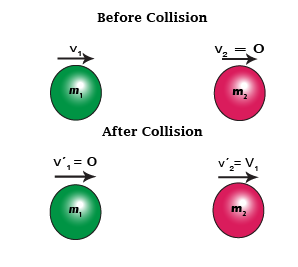
- when m1 = m2 and v2 = 0
 $${v}’_{1} = \frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} $$
$${v}’_{1} = \frac{m_{1}-m_{1}}{m_{1}+m_{1}}v_{1}
$$ $$v'_{1}= 0
$$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{2}}v_{1}
$$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{1}}v_{1}
$$ $$
{v}’_{2} = \frac{2 m_{1}}{2m_{1}}v_{1}
$$ $$
{v}’_{2} = v_{1}
$$
when m1=m2 then ball of mass m1, after collision will come to a stop and m2 will take off with the velocity that m1 originally had before collision.
Thus when a billiard ball m1 moving on a table collides with exactly similar all m2 at rest, the ball m1 stops while m2 begins to move with the same velocity with which m1 was moving initially.
$${v}’_{1} = \frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} $$
$${v}’_{1} = \frac{m_{1}-m_{1}}{m_{1}+m_{1}}v_{1}
$$ $$v'_{1}= 0
$$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{2}}v_{1}
$$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{1}}v_{1}
$$ $$
{v}’_{2} = \frac{2 m_{1}}{2m_{1}}v_{1}
$$ $$
{v}’_{2} = v_{1}
$$
when m1=m2 then ball of mass m1, after collision will come to a stop and m2 will take off with the velocity that m1 originally had before collision.
Thus when a billiard ball m1 moving on a table collides with exactly similar all m2 at rest, the ball m1 stops while m2 begins to move with the same velocity with which m1 was moving initially.
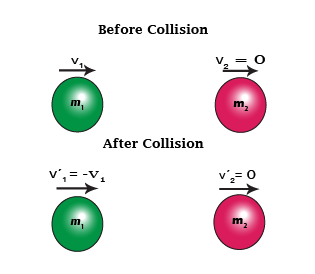
- When a light body collides with massive body at rest
In this case initial velocity v2 = 0 and m2 >> m1.
 $$
v'_{1}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} + \frac{2m_{2}v_{2}}{m_{1}+m_{2}}
$$ $$
As \;\;\;\; m_{1} << m_{2}
$$ $$
and \;\;\;\;\ v_{2}=0
$$ $$
then \;\;\;\;m_{1}- m_{2}= -m_{2} $$ $$
and \;\;\;\;m_{1}+ m_{2}= m_{2} $$ $$
So \; \;
v'_{1}=\frac{-m_{2}}{m_{2}}v_{1} $$ $$
v'_{1} = -v'_{1} $$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{2}}v_{1} +\frac{m_{2}-m_{1}}{m_{1}+m_{2}}v_{2}
$$ $$
As \;\;\;\;m_{1} << m_{2}
$$ $$
and \;\;\;\; v_{2}=0
$$
so
$$
\frac{2 m_{1}}{m_{1}+m_{2}} \widetilde{-}0
$$ $$
{v}’_{2} = 0
$$
Under these conditions m1 can be neglected as compared to m2. From eq 3 we have v’1= - v1 and v’1=0
This means that m1 will bounce back with the same velocity while m2 will remain stationary.
$$
v'_{1}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} + \frac{2m_{2}v_{2}}{m_{1}+m_{2}}
$$ $$
As \;\;\;\; m_{1} << m_{2}
$$ $$
and \;\;\;\;\ v_{2}=0
$$ $$
then \;\;\;\;m_{1}- m_{2}= -m_{2} $$ $$
and \;\;\;\;m_{1}+ m_{2}= m_{2} $$ $$
So \; \;
v'_{1}=\frac{-m_{2}}{m_{2}}v_{1} $$ $$
v'_{1} = -v'_{1} $$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{2}}v_{1} +\frac{m_{2}-m_{1}}{m_{1}+m_{2}}v_{2}
$$ $$
As \;\;\;\;m_{1} << m_{2}
$$ $$
and \;\;\;\; v_{2}=0
$$
so
$$
\frac{2 m_{1}}{m_{1}+m_{2}} \widetilde{-}0
$$ $$
{v}’_{2} = 0
$$
Under these conditions m1 can be neglected as compared to m2. From eq 3 we have v’1= - v1 and v’1=0
This means that m1 will bounce back with the same velocity while m2 will remain stationary.
- When a massive body collides with light stationary body
In this case m1 >> m2 and v2=0 so m2 can be neglected in eq. 3 . This gives v’1 ≈ v1 and v’2 ≈ 2v1.
 Thus after the collision, there is practically no change in the velocity of the massive body, but the lighter on bounces off tin the forward direction with approximately double the velocity of the incident body.
$$
v'_{1}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} + \frac{2m_{2}v_{2}}{m_{1}+m_{2}}
$$ $$
m_{1} >> m_{2}
$$ $$
m_{1}-m_{2} \widetilde{-} m_{1}
$$ $$
\frac{2m_{2}v_{2}}{m_{1}+m_{2}} \widetilde{-}0
$$ $$
v'_{1}=\frac{m_{1}}{m_{1}}v_{1} + 0
$$ $$
v'_{1}=v_{1} $$
Similarly
$$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{2}}v_{1} +\frac{m_{2}-m_{1}}{m_{1}+m_{2}}v_{2}
$$ $$
m_{1} >> m_{2}
$$ $$
m_{1}+m_{2} \widetilde{-} m_{1}
$$ $$
\frac{m_{2}-m_{1}}{m_{1}+m_{2}} \widetilde{-}0
$$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}}v_{1}
$$ $$
{v}’_{2} = 2 v_{1}
$$
Thus after the collision, there is practically no change in the velocity of the massive body, but the lighter on bounces off tin the forward direction with approximately double the velocity of the incident body.
$$
v'_{1}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} + \frac{2m_{2}v_{2}}{m_{1}+m_{2}}
$$ $$
m_{1} >> m_{2}
$$ $$
m_{1}-m_{2} \widetilde{-} m_{1}
$$ $$
\frac{2m_{2}v_{2}}{m_{1}+m_{2}} \widetilde{-}0
$$ $$
v'_{1}=\frac{m_{1}}{m_{1}}v_{1} + 0
$$ $$
v'_{1}=v_{1} $$
Similarly
$$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{2}}v_{1} +\frac{m_{2}-m_{1}}{m_{1}+m_{2}}v_{2}
$$ $$
m_{1} >> m_{2}
$$ $$
m_{1}+m_{2} \widetilde{-} m_{1}
$$ $$
\frac{m_{2}-m_{1}}{m_{1}+m_{2}} \widetilde{-}0
$$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}}v_{1}
$$ $$
{v}’_{2} = 2 v_{1}
$$
 Consider two smooth non-rotating balls of masses m1 mass m2 moving initially with velocities v1 and v2 in the same direction.
We assume that v1 > v2 .
Therefore m1 will come close to m2 and will collide with it.
After collision they move along the same straight line without rotation. Let their velocities after the collision be v’1 and v’2 respectively.
Consider two smooth non-rotating balls of masses m1 mass m2 moving initially with velocities v1 and v2 in the same direction.
We assume that v1 > v2 .
Therefore m1 will come close to m2 and will collide with it.
After collision they move along the same straight line without rotation. Let their velocities after the collision be v’1 and v’2 respectively.  $$
v'_{1}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} + \frac{2m_{2}v_{2}}{m_{1}+m_{2}}
$$ $$
v'_{1}=\frac{m_{1}-m_{1}}{m_{1}+m_{1}}v_{1} + \frac{2m_{1}v_{2}}{m_{1}+m_{1}}
$$ $$
v'_{1}=\frac{0}{m_{1}+m_{1}}v_{1} + \frac{2m_{1}v_{2}}{2m_{1}}$$
from above equations we find that
$$ {v}’_{1} = v_{2}$$
and $$ {v}’_{2} = v_{1}$$
$$
v'_{1}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} + \frac{2m_{2}v_{2}}{m_{1}+m_{2}}
$$ $$
v'_{1}=\frac{m_{1}-m_{1}}{m_{1}+m_{1}}v_{1} + \frac{2m_{1}v_{2}}{m_{1}+m_{1}}
$$ $$
v'_{1}=\frac{0}{m_{1}+m_{1}}v_{1} + \frac{2m_{1}v_{2}}{2m_{1}}$$
from above equations we find that
$$ {v}’_{1} = v_{2}$$
and $$ {v}’_{2} = v_{1}$$
 $${v}’_{1} = \frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} $$
$${v}’_{1} = \frac{m_{1}-m_{1}}{m_{1}+m_{1}}v_{1}
$$ $$v'_{1}= 0
$$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{2}}v_{1}
$$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{1}}v_{1}
$$ $$
{v}’_{2} = \frac{2 m_{1}}{2m_{1}}v_{1}
$$ $$
{v}’_{2} = v_{1}
$$
when m1=m2 then ball of mass m1, after collision will come to a stop and m2 will take off with the velocity that m1 originally had before collision.
Thus when a billiard ball m1 moving on a table collides with exactly similar all m2 at rest, the ball m1 stops while m2 begins to move with the same velocity with which m1 was moving initially.
$${v}’_{1} = \frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} $$
$${v}’_{1} = \frac{m_{1}-m_{1}}{m_{1}+m_{1}}v_{1}
$$ $$v'_{1}= 0
$$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{2}}v_{1}
$$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{1}}v_{1}
$$ $$
{v}’_{2} = \frac{2 m_{1}}{2m_{1}}v_{1}
$$ $$
{v}’_{2} = v_{1}
$$
when m1=m2 then ball of mass m1, after collision will come to a stop and m2 will take off with the velocity that m1 originally had before collision.
Thus when a billiard ball m1 moving on a table collides with exactly similar all m2 at rest, the ball m1 stops while m2 begins to move with the same velocity with which m1 was moving initially.  $$
v'_{1}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} + \frac{2m_{2}v_{2}}{m_{1}+m_{2}}
$$ $$
As \;\;\;\; m_{1} << m_{2}
$$ $$
and \;\;\;\;\ v_{2}=0
$$ $$
then \;\;\;\;m_{1}- m_{2}= -m_{2} $$ $$
and \;\;\;\;m_{1}+ m_{2}= m_{2} $$ $$
So \; \;
v'_{1}=\frac{-m_{2}}{m_{2}}v_{1} $$ $$
v'_{1} = -v'_{1} $$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{2}}v_{1} +\frac{m_{2}-m_{1}}{m_{1}+m_{2}}v_{2}
$$ $$
As \;\;\;\;m_{1} << m_{2}
$$ $$
and \;\;\;\; v_{2}=0
$$
so
$$
\frac{2 m_{1}}{m_{1}+m_{2}} \widetilde{-}0
$$ $$
{v}’_{2} = 0
$$
Under these conditions m1 can be neglected as compared to m2. From eq 3 we have v’1= - v1 and v’1=0
This means that m1 will bounce back with the same velocity while m2 will remain stationary.
$$
v'_{1}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} + \frac{2m_{2}v_{2}}{m_{1}+m_{2}}
$$ $$
As \;\;\;\; m_{1} << m_{2}
$$ $$
and \;\;\;\;\ v_{2}=0
$$ $$
then \;\;\;\;m_{1}- m_{2}= -m_{2} $$ $$
and \;\;\;\;m_{1}+ m_{2}= m_{2} $$ $$
So \; \;
v'_{1}=\frac{-m_{2}}{m_{2}}v_{1} $$ $$
v'_{1} = -v'_{1} $$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{2}}v_{1} +\frac{m_{2}-m_{1}}{m_{1}+m_{2}}v_{2}
$$ $$
As \;\;\;\;m_{1} << m_{2}
$$ $$
and \;\;\;\; v_{2}=0
$$
so
$$
\frac{2 m_{1}}{m_{1}+m_{2}} \widetilde{-}0
$$ $$
{v}’_{2} = 0
$$
Under these conditions m1 can be neglected as compared to m2. From eq 3 we have v’1= - v1 and v’1=0
This means that m1 will bounce back with the same velocity while m2 will remain stationary.
 Thus after the collision, there is practically no change in the velocity of the massive body, but the lighter on bounces off tin the forward direction with approximately double the velocity of the incident body.
$$
v'_{1}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} + \frac{2m_{2}v_{2}}{m_{1}+m_{2}}
$$ $$
m_{1} >> m_{2}
$$ $$
m_{1}-m_{2} \widetilde{-} m_{1}
$$ $$
\frac{2m_{2}v_{2}}{m_{1}+m_{2}} \widetilde{-}0
$$ $$
v'_{1}=\frac{m_{1}}{m_{1}}v_{1} + 0
$$ $$
v'_{1}=v_{1} $$
Similarly
$$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{2}}v_{1} +\frac{m_{2}-m_{1}}{m_{1}+m_{2}}v_{2}
$$ $$
m_{1} >> m_{2}
$$ $$
m_{1}+m_{2} \widetilde{-} m_{1}
$$ $$
\frac{m_{2}-m_{1}}{m_{1}+m_{2}} \widetilde{-}0
$$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}}v_{1}
$$ $$
{v}’_{2} = 2 v_{1}
$$
Thus after the collision, there is practically no change in the velocity of the massive body, but the lighter on bounces off tin the forward direction with approximately double the velocity of the incident body.
$$
v'_{1}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}}v_{1} + \frac{2m_{2}v_{2}}{m_{1}+m_{2}}
$$ $$
m_{1} >> m_{2}
$$ $$
m_{1}-m_{2} \widetilde{-} m_{1}
$$ $$
\frac{2m_{2}v_{2}}{m_{1}+m_{2}} \widetilde{-}0
$$ $$
v'_{1}=\frac{m_{1}}{m_{1}}v_{1} + 0
$$ $$
v'_{1}=v_{1} $$
Similarly
$$
{v}’_{2} = \frac{2 m_{1}}{m_{1}+m_{2}}v_{1} +\frac{m_{2}-m_{1}}{m_{1}+m_{2}}v_{2}
$$ $$
m_{1} >> m_{2}
$$ $$
m_{1}+m_{2} \widetilde{-} m_{1}
$$ $$
\frac{m_{2}-m_{1}}{m_{1}+m_{2}} \widetilde{-}0
$$ $$
{v}’_{2} = \frac{2 m_{1}}{m_{1}}v_{1}
$$ $$
{v}’_{2} = 2 v_{1}
$$